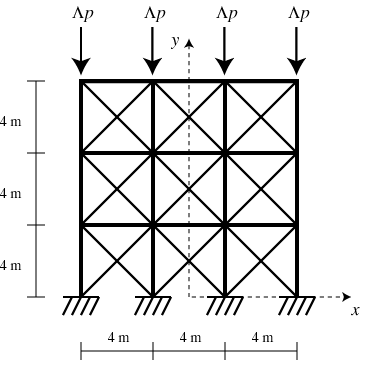
３層３スパンの骨組構造物

Λをパラメータとして比例載荷する。 骨組が座屈するときのΛの値は座屈荷重係数と呼ばれる。 いま、正の座屈荷重係数がある最小制限値以上である、という制約を設ける。 断面積を設計変数として、構造物の総部材体積を最小になるような断面積を求め る。この問題の解は次のようになる。

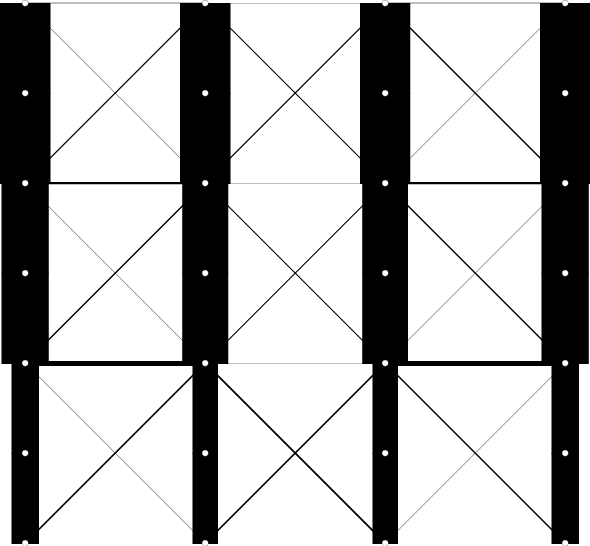
最適解

本最適化問題は、断面積の関数として定められる実対称行列が半正定値であると いう制約の下で、総部材体積を最小化する問題に帰着できる。 さらにこの問題をＳＤＰとして逐次近似し、繰り返しＳＤＰを解くことで最適解 を簡単に求めることができる。 最適解では、次の４つの座屈モードが重複している。

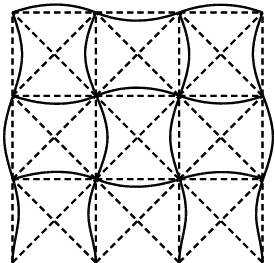
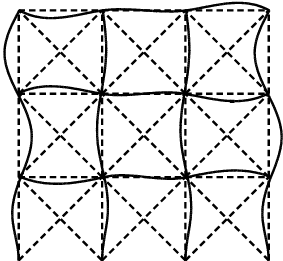
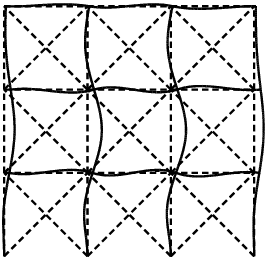
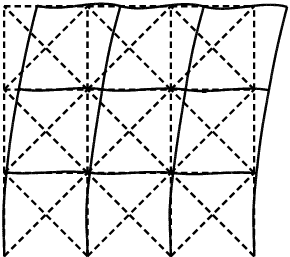
座屈モード

この座屈モードの重複のために、既往の手法で解を求めることは極めて困難であ る。 しかし、ＳＤＰを用いて解を得る手法では、容易に最適解を得ることができる。
骨組構造物では、通常、上層の柱の断面積が下層のそれよりも大きくなるような 設計はしない。 そこで、上層の柱の断面積は、下層の柱の断面積以下であるという制約を設けて 最適化を行うと、次のような最適解を得ることが出来る。

最適解

このとき、最適解では次の３つの座屈モードが重複している。

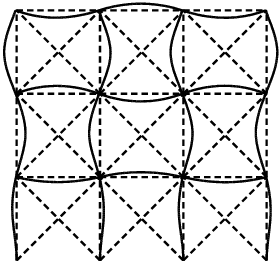
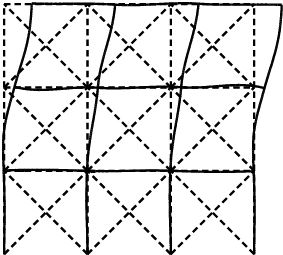
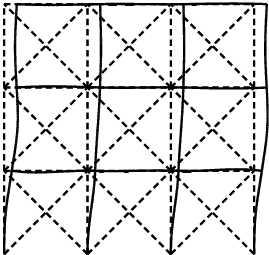
座屈モード

このように、対称なnon-swayモードと、逆対称な２つのswayモードが重複してい る。
座屈荷重制約条件下での骨組の最適設計については、これまでに、swayモードと non-swayモードの２つが重複することは知られていた。 しかし、ここで示したように、３つ以上のモードが重複することは知られていな いようであるので、これらの結果は非常に興味深い。 このように多数の座屈モードが重複する結果を得ることができるのは、ＳＤＰを 用いて最適設計問題を解くと、座屈荷重係数の重複に関係なく、最適解を得るこ とができるからである。