□□Research Topics□□

固有１次振動数を制約条件として、トラス構造物を最適化する。次のような正方形平面トラスを考える。

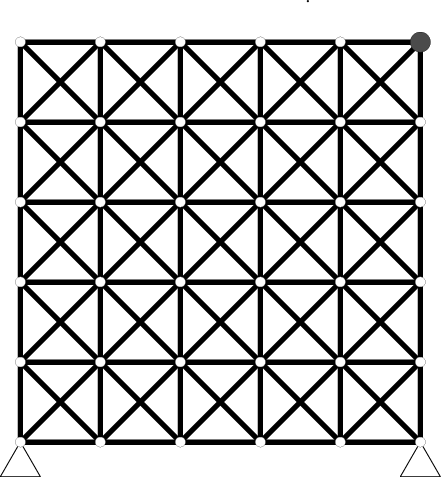
５×５正方形平面トラス

固有振動数が最小制限値以上である、という制約を設ける。断面積を設計変数として、構造物の総部材体積を最小になるような断面積を求める。右上の１節点のみに集中質量（非構造質量）が存在する場合、最適解は次のように得られる。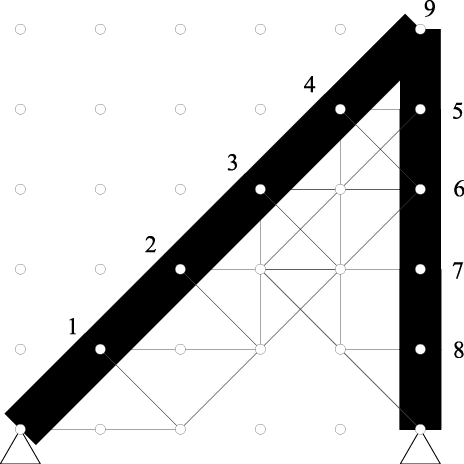

正方形平面トラスの最適トポロジー

本最適化問題は、ＳＤＰ問題に帰着することができる。そこで、ＳＤＰに対する有効な解法である、主双対内点法を用いることで、最適トポロジーを困難なく求めることができる。
この最適解では、２つの固有モードが重複している。

次に、アーチ状の平面トラスを考える。非構造質量は、最下層の全ての節点に存在する。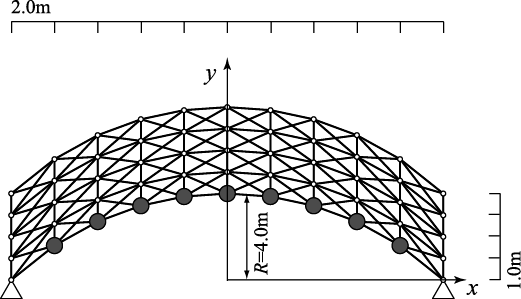

５５節点アーチ状平面トラス

このとき、次のような最適解が得られる。最適解における１次固有値の重複度は２である。これらは、それぞれ対称モードと逆対称モードに対応している。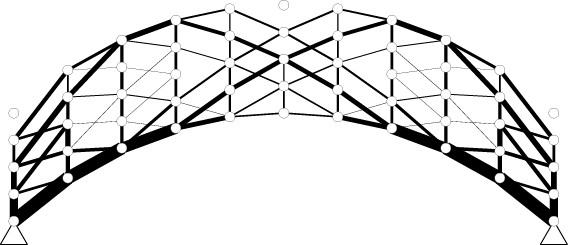

５５節点アーチ状平面トラスの最適トポロジー

最後に、次のような立体トラスの最適トポロジーを求めてみる。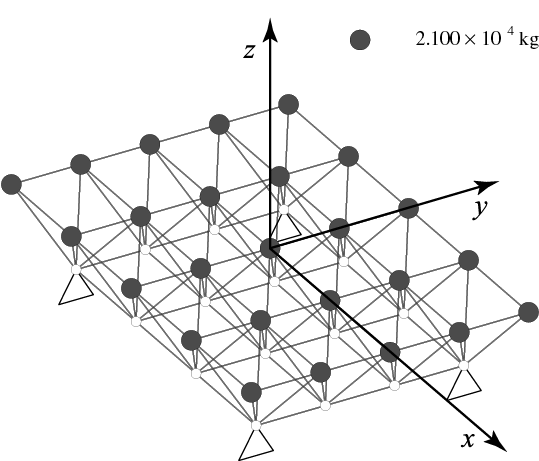

２層平板状立体トラス

最適トポロジーは次のようになる。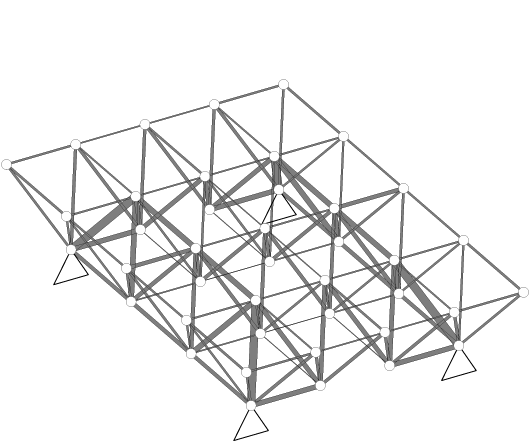

２層平板状立体トラスの最適トポロジー

この最適解では、５つの固有モードが重複している。
このように多くの１次固有値が重複する場合にも、提案手法では困難なく解を得ることが出来る。